Plugin information
| Version | 0.3.0 |
|---|---|
| Author | Dataiku (Liev GARCIA, Thibault DESFONTAINES, Alex COMBESSIE) |
| Released | 2020-11 |
| Last updated | 2023-08 |
| License | Apache Software License |
| Source code | Github |
| Reporting issues | Github |
With this plugin, you will be able to:
- Build the index required to search for nearest neighbors
- Find the nearest neighbors of each row of a dataset using a pre-computed index
Note that this plugin requires at least DSS version 8.0.2.
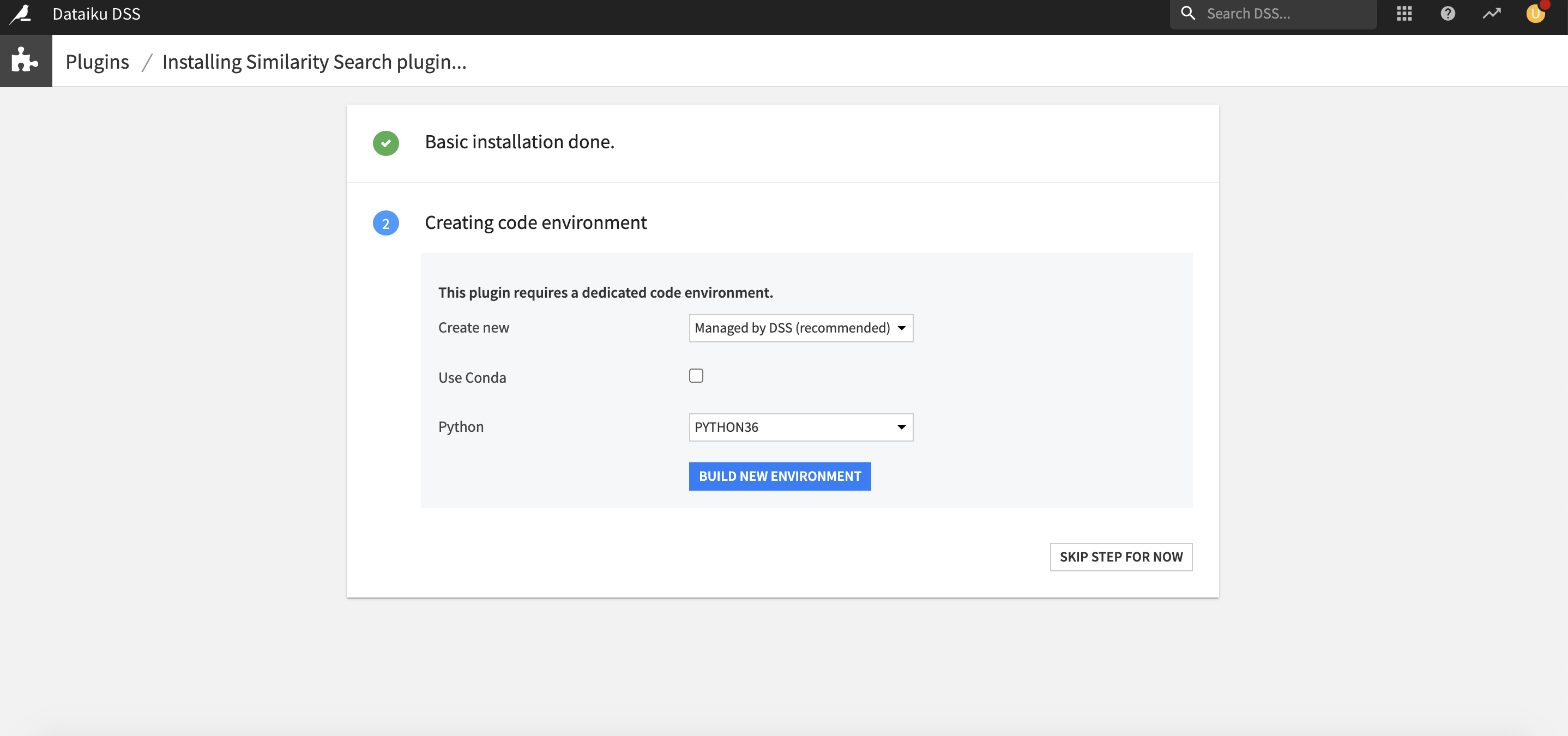
How to set up
Right after installing the plugin, you will need to build its code environment. Note that this plugin requires Python version 3.6 and that conda is not supported.
How to use
To use this plugin, you need to have a dataset with:
- One column to identify your items
- Numeric columns which represent these items, which can combine
- Simple numeric columns with integer or decimal values
- Vector columns with embeddings* computed from Deep Learning models
In this documentation, we will work on image data as an example, using the Deep Learning for Images plugin to compute embeddings. If you have text data, you can also leverage the Sentence Embedding plugin. Alternatively, you can use your numeric columns directly or compute embeddings with your own code.
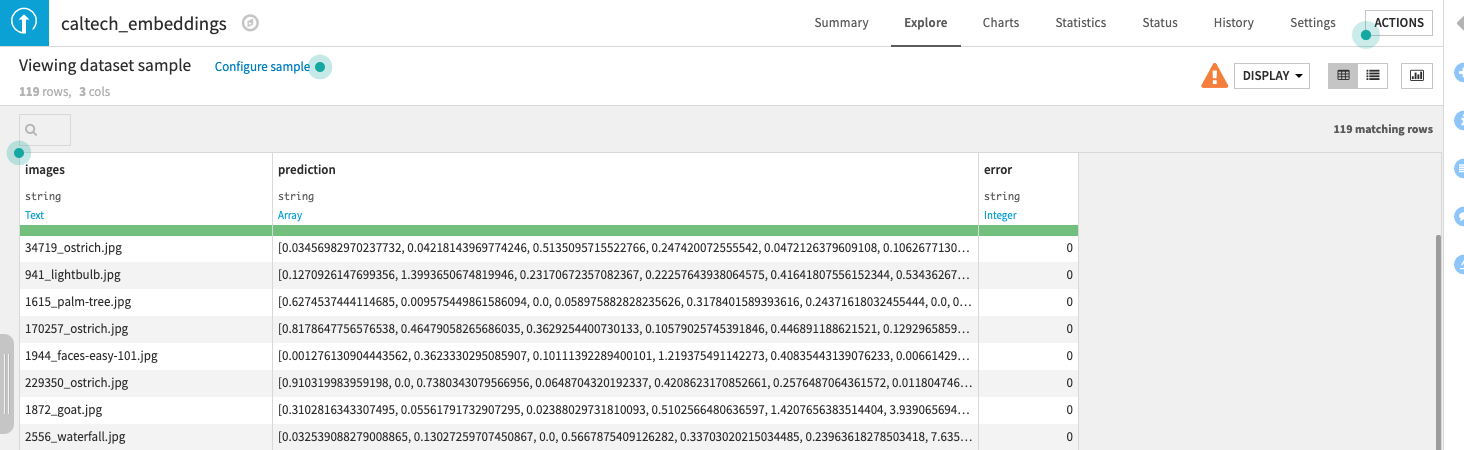
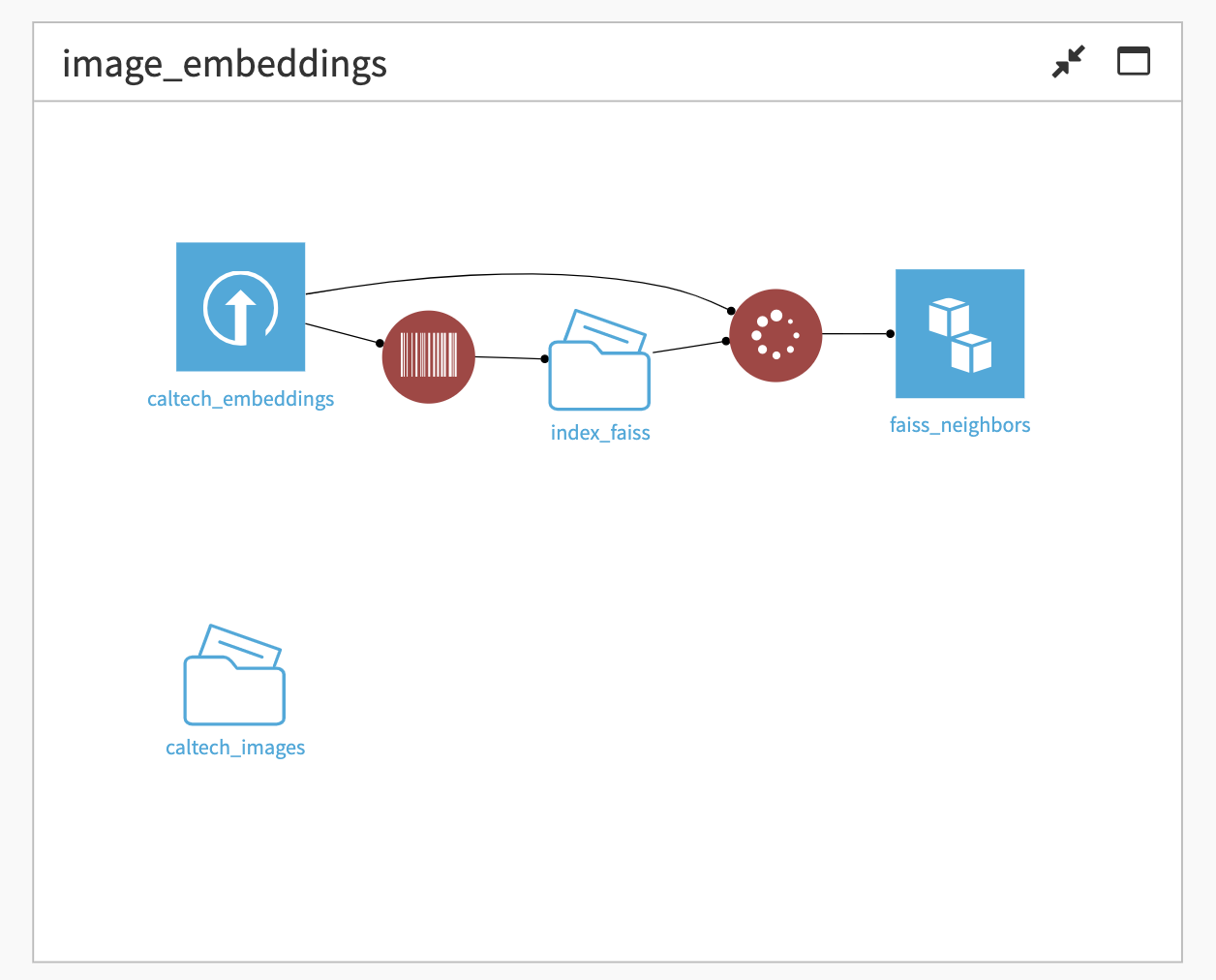
Once your dataset is ready, navigate to the Flow and select the Similarity Search plugin from the +RECIPE dropdown menu under the Recommender System category. If your dataset is selected in the Flow, you can directly find the plugin on the right panel.
This plugin contains two recipes, Build Nearest Neighbor Search Index and Find Nearest Neighbors.
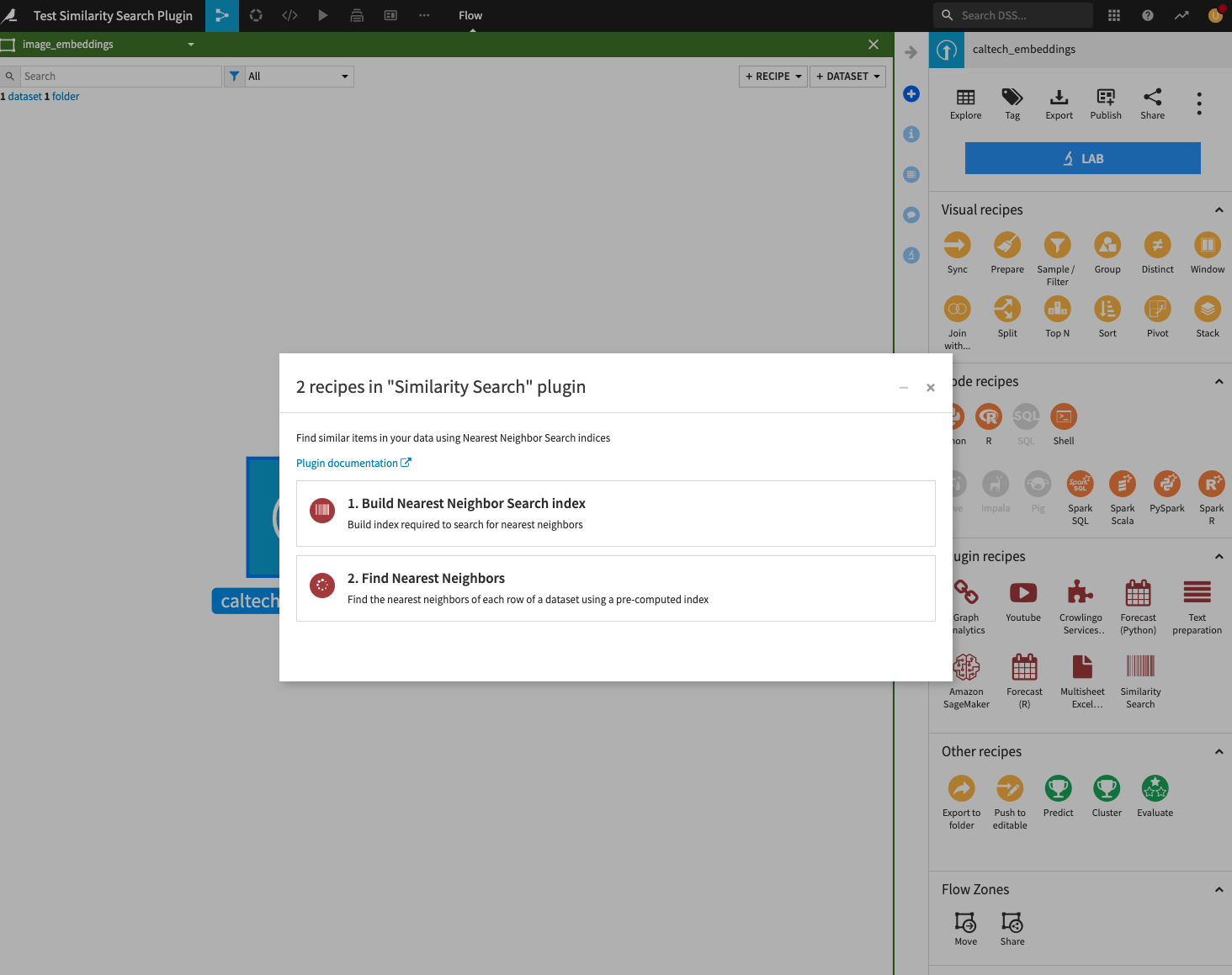
1. Build Nearest Neighbor Search Index
Build index required to search for nearest neighbors
Input
- Dataset containing numeric or vector data (e.g. embeddings)
Output
- Folder where the index will be saved
Settings
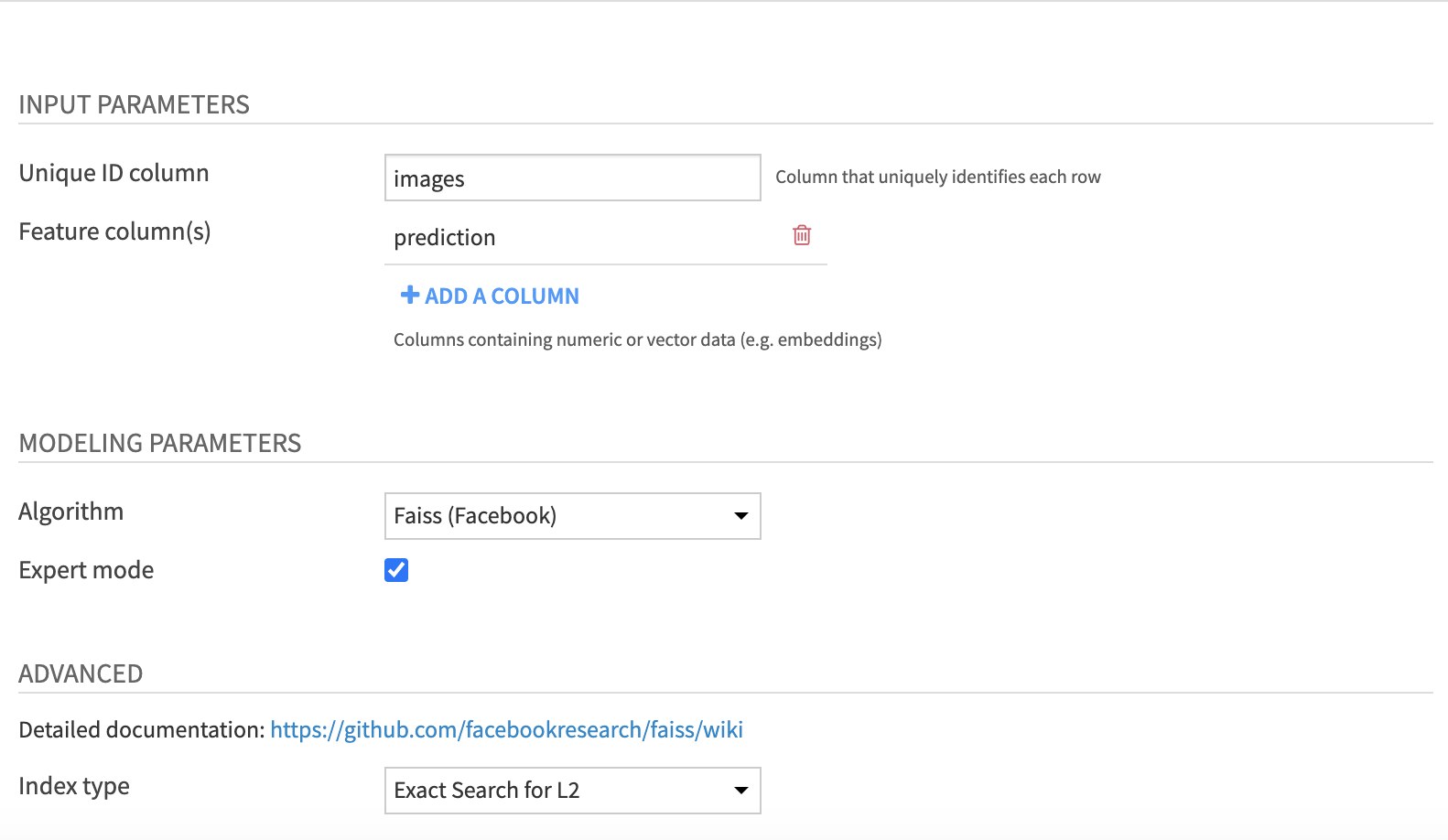
Input parameters
- Unique ID column which uniquely identifies each row
- Feature column(s) with numeric or vector data (e.g. embeddings)
Note
To address memory issues, the feature column(s) must not contain vectors longer than 65,536 = 2^16.
Modeling parameters
- Algorithm: Choose Annoy (Spotify) or Faiss (Facebook)
- Expert mode: If activated, display Advanced parameters depending on the chosen algorithm
- Annoy: Distance metric and Number of trees according to this documentation
- Faiss: Index type and Number of LSH bits (if Index type is Locality-Sensitive Hashing) according to this documentation
2. Find Nearest Neighbors
Find the nearest neighbors of each row of a dataset using a pre-computed index
Input
- Dataset containing numeric or vector data (e.g. embeddings) – May be different from the one used to build indices
- Folder containing a pre-computed index
Output
- Dataset with identified nearest neighbors for each row
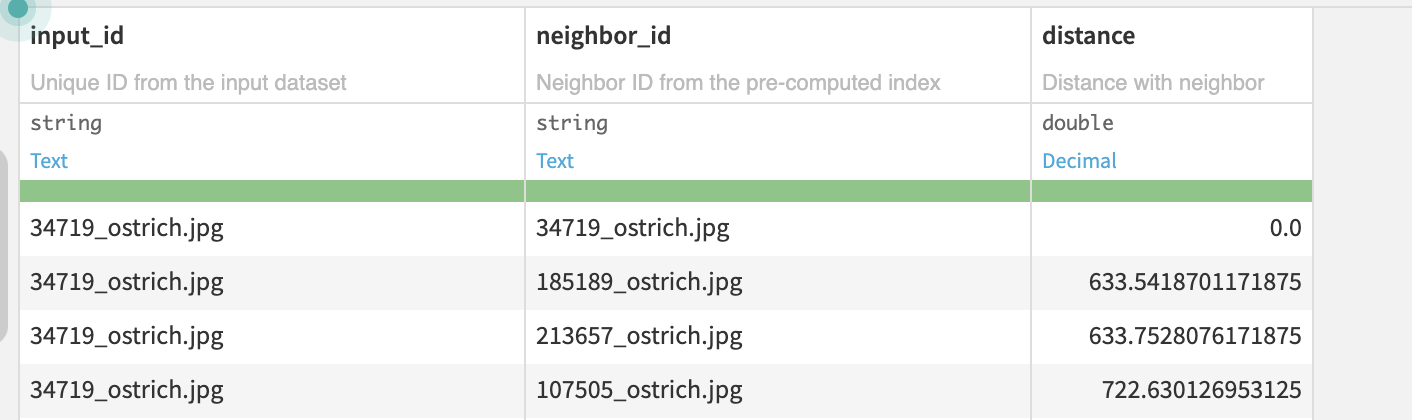
Settings
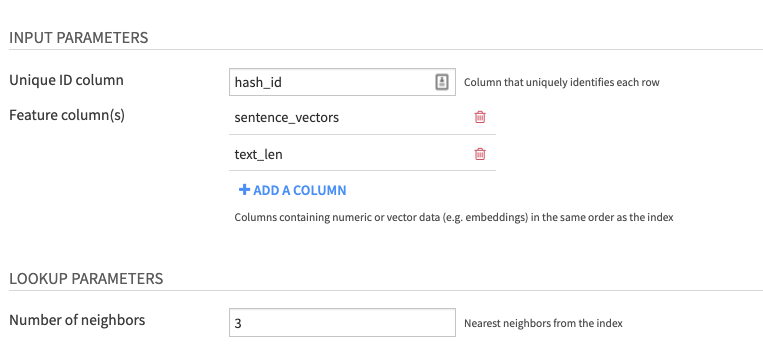
Input parameters
- Unique ID column which uniquely identifies each row
- Feature column(s) with numeric or vector data (e.g. embeddings) in the same order as the index
- You can check the order of columns used in the index in the output folder of the previous recipe, inside the config.json file
Note
To address memory issues, the feature column(s) must not contain vectors longer than 65,536 = 2^16.
Lookup parameters
- Number of Neighbors: Choose how many nearest neighbors to retrieve from the pre-computed index
To conclude
With these two recipes, you can build simple yet powerful recommender systems to answer real-life use cases. If you run a support team, you can help your agents find similar tickets to the ones they are working on. If you run an e-commerce website, you can help your users find similar products to the one they are looking for.
Happy similarity search!
For the curious ones
* An embedding is a multi-dimensional space that is used to represent complex objects like images, videos, texts, or sounds. Neural networks used for text classification or image recognition, for example, are learning embeddings in their hidden layers to produce an actual prediction. In terms of geometry, items that are similar with respect to a prediction task will be close to one another in terms of distance in the embedding space.